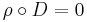Courant algebroid
In a field of mathematics known as differential geometry, a Courant algebroid is a combination of a Lie algebroid and a quadratic Lie algebra. It was originally introduced in 1990 by Theodore James Courant in his dissertation at UC Berkeley where he first called them Dirac Manifolds, and then were re-named after him in 1997 by Zhang-Ju Liu, Alan Weinstein and Ping Xu to describe the double of a Lie bialgebroid.
Contents |
Definition
A Courant algebroid consists of the data a vector bundle 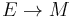 with a bracket
with a bracket ![[.,.]:\Gamma E \times \Gamma E \to \Gamma E](/2012-wikipedia_en_all_nopic_01_2012/I/3199e04936112e020f02840aef203ac2.png) , a non degenerate inner product
, a non degenerate inner product 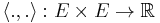 , and a bundle map
, and a bundle map 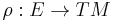 subject to the following axioms,
subject to the following axioms,
where φ,ψ are sections into E and f is a smooth function on the base manifold M. D is the combination 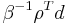 with d the de Rham differential,
with d the de Rham differential, 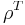 the dual map of
the dual map of  , and β the map from E to
, and β the map from E to 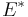 induced by the metric.
induced by the metric.
Properties
The bracket is not skew-symmetric as one can see from the third axiom. Instead it fulfils a certain Jacobi-identity (first axiom) and a Leibniz rule (second axiom). From these two axioms one can derive that the anchor map ρ is a morphism of brackets:
The fourth rule is an invariance of the inner product under the bracket. Polarization leads to
Examples
An example of the Courant algebroid is the Dorfman bracket on the direct sum 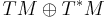 with a twist introduced by Ševera, defined as:
with a twist introduced by Ševera, defined as:
where X,Y are vector fields, ξ,η are 1-forms and H is a closed 3-form twisting the bracket. This bracket is used to describe the integrability of generalized complex structures.
A more general example arises from a Lie algebroid A whose induced differential on 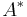 will be written as d again. Then use the same formula as for the Dorfman bracket with H an A-3-form closed under d.
will be written as d again. Then use the same formula as for the Dorfman bracket with H an A-3-form closed under d.
Another example of a Courant algebroid is a quadratic Lie algebra, i.e. a Lie algebra with an invariant scalar product. Here the base manifold is just a point and thus the anchor map (and D) are trivial.
The example described in the paper by Weinstein et al. comes from a Lie bialgebroid, i.e. A a Lie algebroid (with anchor 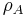 and bracket
and bracket ![[.,.]_A](/2012-wikipedia_en_all_nopic_01_2012/I/34711a18a1eaf9cb18af9a6c401bd994.png) ), also its dual
), also its dual 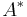 a Lie algebroid (inducing the differential
a Lie algebroid (inducing the differential 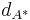 on
on  ) and
) and ![d_{A^*}[X,Y]_A=[d_{A^*}X,Y]_A-[X,d_{A^*}Y]_A](/2012-wikipedia_en_all_nopic_01_2012/I/c29e78370c22fcad4de459f1b3189435.png) (where on the RHS you extend the A-bracket to
(where on the RHS you extend the A-bracket to  using graded Leibniz rule). This notion is symmetric in A and
using graded Leibniz rule). This notion is symmetric in A and 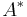 (see Roytenberg). Here
(see Roytenberg). Here 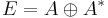 with anchor
with anchor 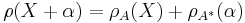 and the bracket is the skew-symmetrization of the above in X and α (equivalently in Y and β):
and the bracket is the skew-symmetrization of the above in X and α (equivalently in Y and β):
Skew-symmetric bracket
Instead of the definition above one can introduce a skew-symmetric bracket as
This fulfils a homotopic Jacobi-identity.
where T is
The Leibniz rule and the invariance of the scalar product become modified by the relation ![[[\phi,\psi]] = [\phi,\psi] -\frac12 D\langle \phi,\psi\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/84693d3ea06702a8e785332317567085.png) and the violation of skew-symmetry gets replaced by the axiom
and the violation of skew-symmetry gets replaced by the axiom
The skew-symmetric bracket together with the derivation D and the Jacobiator T form a strongly homotopic Lie algebra.
References
- Liu, Weinstein, and Xu: Manin triples for Lie Bialgebroids, Journ. of Diff.geom. 45 pp.647–574 (1997)
- Dmitry Roytenberg: Courant algebroids, derived brackets, and even symplectic supermanifolds, PhD thesis Univ. of California Berkeley (1999)
- Pavol Ševera: Letters to A. Weinstein, unpublished (1998)
![[\phi, [\chi, \psi]] = [[\phi, \chi], \psi] %2B [\chi, [\phi, \psi]]](/2012-wikipedia_en_all_nopic_01_2012/I/96440034b8bd43db006df20ea69f77ba.png)
![[\phi, f\psi] = \rho(\phi)f\psi %2Bf[\phi, \psi]](/2012-wikipedia_en_all_nopic_01_2012/I/cd7aa7dcab2beab15e0ece602715171b.png)
![[\phi,\phi]= \frac12 D\langle \phi,\phi\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/1ccfcdc77b3b4b4b2a1b5c0841e5bd02.png)
![\rho(\phi)\langle \psi,\psi\rangle= 2\langle [\phi,\psi],\psi\rangle](/2012-wikipedia_en_all_nopic_01_2012/I/7c0cc3e03f97cf79c50e89c94b09137e.png)
![\rho[\phi,\psi] = [\rho(\phi),\rho(\psi)] .](/2012-wikipedia_en_all_nopic_01_2012/I/6a15ae2f6a3c0896414dec54a2d6bbc3.png)
![\rho(\phi)\langle \chi,\psi\rangle= \langle [\phi,\chi],\psi\rangle %2B\langle \chi,[\phi,\psi]\rangle .](/2012-wikipedia_en_all_nopic_01_2012/I/85773b83bcec386c4a45a3e31246eb55.png)
![[X%2B\xi, Y%2B\eta] = [X,Y]%2B(\mathcal{L}_X\eta -i(Y) d\xi %2Bi(X)i(Y)H)](/2012-wikipedia_en_all_nopic_01_2012/I/fe1868ef88b7ed269ab60b4a780959ee.png)
![[X%2B\alpha,Y%2B\beta]= ([X,Y]_A %2B\mathcal{L}^{A^*}_{\alpha}Y-i_\beta d_{A^*}X) %2B([\alpha,\beta]_{A^*} %2B\mathcal{L}^A_X\beta-i_Yd_{A}\alpha)](/2012-wikipedia_en_all_nopic_01_2012/I/37052884de0e85850dca9b346c05d06f.png)
![[[\phi,\psi]]= \frac12\big([\phi,\psi]-[\psi,\phi]\big.)](/2012-wikipedia_en_all_nopic_01_2012/I/26e1e52c98606fd2f83586c4aae09168.png)
![[[\phi,[[\psi,\chi]]\,]] %2B\text{cycl.} = DT(\phi,\psi,\chi)](/2012-wikipedia_en_all_nopic_01_2012/I/60b88e4c51c064909479308c4e951de5.png)
![T(\phi,\psi,\chi)=\frac13\langle [\phi,\psi],\chi\rangle %2B\text{cycl.}](/2012-wikipedia_en_all_nopic_01_2012/I/f674c5b49d3f73614e6d98394a6f43cc.png)